Circunferencia de los nueve puntos

En geometría, se conoce como circunferencia de los nueve puntos aquella que se puede construir con puntos vinculados a cualquier triángulo propuesto. Su nombre deriva del hecho que la circunferencia pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo (salvo que el triángulo sea obtusángulo aunque también existen). Estos son:

los puntos medios de los tres lados del triángulo,
los pies de las alturas de tal triángulo,
los puntos medios de los segmentos que unen los tres vértices con el ortocentro del triángulo.

Historia

Generalmente, se adjudica al alemán Karl Wilhelm Feuerbach el descubrimiento de la circunferencia de los nueve puntos; sin embargo, lo que él descubrió fue la circunferencia de los seis puntos, reconociendo que sobre ella se encontraban los puntos medios de los lados de un triángulo y los pies de las alturas (en la figura, los puntos: M N P y E G J).

Anteriormente, Charles Brianchon y Jean-Victor Poncelet habían demostrado el mismo teorema. Poco tiempo después de Feuerbach, el matemático Olry Terquem también demostró la existencia del círculo y reconoció además que los puntos medios de los segmentos determinados por los vértices del triángulo y el ortocentro, también estaban contenidos en la circunferencia (en la figura, los puntos: D, F, H).

Onomástica

Poncelet la llamó circunferencia de los nueve puntos, denominación generalmente usada en los países de habla inglesa. Algunos geómetras franceses la llaman círculo de Euler ( o circunferencia de Euler) y los geómetras teutones la denominan circunferencia de Feuerbach, y en México, circunferencia de los nueve puntos (sic).^[1] Charles Wexler lo presenta como un teorema notable de geometría moderna e indica sus propiedades.^[2] Pero en la obra de Shively, en la primera edición en castellano, en Latinoamérica, ya se conocía con el nombre de la "circunferencia de los nueve puntos" ^[3]

Teorema

Dado un triángulo, hay una circunferencia que pasa por los puntos medios de los lados, los pies de las alturas y los puntos que bisecan los segmentos que unen sus vértices con el ortocentro.^[4]

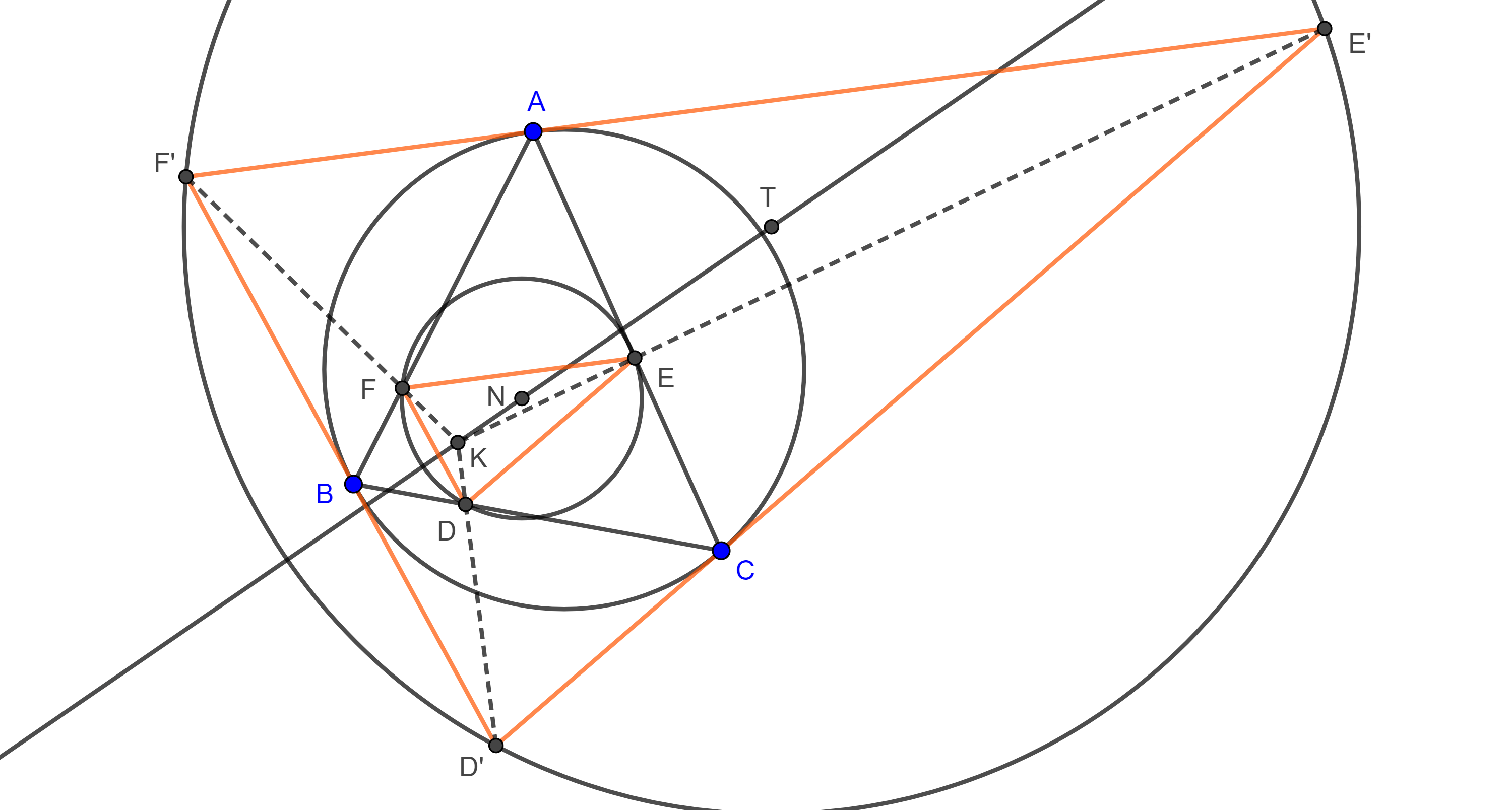
Circunferencia circunscrita y la de Feuerbach

Por la observación de que los puntos D, F y H satisfacen

${\text{IA}}=2\,{\text{ID}}\,\quad {\text{IB}}=2\,{\text{IF}}\,\quad {\text{IC}}=2\,{\text{IH}},$

se deduce que:

la circunferencia de Feuerbach de un triángulo es homotética a la circunferencia circunscrita,
el centro de homotecia es el ortocentro del triángulo,
la razón de la homotecia es 2.

El triángulo formado por los puntos D, F y H^[5] es semejante al triángulo ABC. También se observa que el centro de la circunferencia de Feuerbach N, es punto medio del segmento IO, donde O es el circuncentro del triángulo ABC.

Finalmente, el centro de la circunferencia de Feuerbach se halla sobre la recta de Euler del triángulo.

Otras propiedades

En 1822, Karl Wilhelm Feuerbach descubrió una de las propiedades más profundas sobre la circunferencia que lleva su nombre: la circunferencia de los nueve puntos es tangente exterior a los círculos exinscritos al triángulo. La circunferencia inscrita al triángulo es tangente interior a la circunferencia de Feuerbach.

La demostración de este hecho^[6] puede hacerse, observando que los puntos de tangencia de dos de las circunferencias exinscritas a uno de los lados del triángulo equidistan del punto medio de dicho lado. Usando la inversión respecto de este punto medio se le puede dar el toque final a la demostración.